20pts

观察$w_i$等于0的时候只可以看见$s==t$的点,$s==t$的时候只能被$w_i=0$的点看见，所以可以过前4个数据.

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10;
int w[N],ans[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<n;i++)
    {
        int a,b;
        cin>>a>>b;
    }
    for(int i=1;i<=n;i++)
    {
        cin>>w[i];
    }
    while(m--)
    {
        int a,b;
        cin>>a>>b;
        if(w[a]==0) ans[a]++; //观察员到的时候,a开始走的时候
    }
    for(int i=1;i<=n;i++)
    {
        cout<<ans[i]<<" ";
    }
    return 0;
}

100pts

推导性质

通过分析，可以得到以下性质：

1. 起点到终点的路径只有一条。
2. 在起点 $s_i$ 到终点 $t_i$ 的过程中，会在 $LCA(s_i, t_i)$这个节点发生转折。
3. 可以将一条路径剖分为两条链，剖分的地方是 $LCA(s_i, t_i)$。

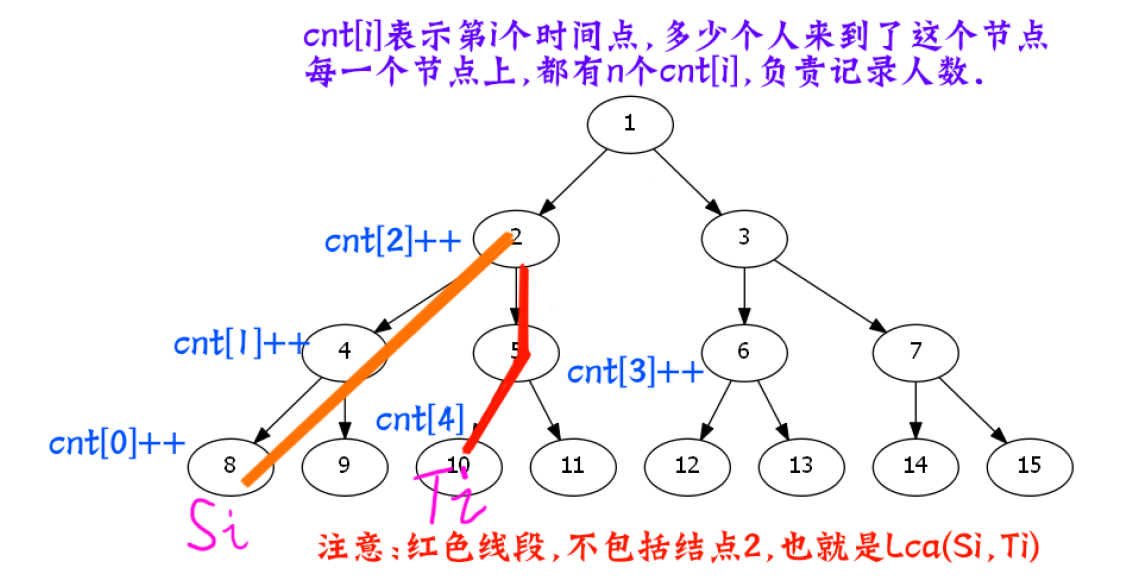
分类讨论

上升链

对于上升链（从 $s_i$ 到 $LCA(s_i, t_i)$）：

• 一个观察员可以看到的人，一定是在时间 $= w_i$ 抵达该节点的人。
• 刚好在时间 $w_i$ 抵达该节点的人，满足条件：

$d[s_i] - w_i = d[x]$

下降链

对于上升链（从 $LCA(s_i, t_i)$ 到 $t_i$）：

• 一个观察员可以看到的人，一定是在时间 $= w_i$ 抵达该节点的人。
• 刚好在时间 $w_i$ 抵达该节点的人，满足条件：

$d[s_i] = w_i + 2 × d[LCA(s_i, t_i)] - d[x]$

对于上升链,有 m 个玩家，其中第 i 个玩家，在 $s_i$ 到 $LCA(s_i, t_i)$ 路径上的每个点增加一个类型为 $d[s_i]$ 的物品。

最终统计点 $x$ 有多少个 $W[x] + d[x]$ 物品。

对于每个点增加，我们可以使用差分将$s_i$到 $LCA(s_i,t_i)$更新，最终我们只需要遍历整棵树即可.

val = c[W[x] + d[x]] // 遍历这个节点前，它已经有的物品

// 遍历所有子树节点后，它已经有的物品

c[W[x] + d[x]] = 新的值

// 然后树上差分

c[W[x] + d[x]] -= val

对于下降的链同理

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
const int N=300010,M=N*2,K=19;
int n,m;
int h[N],e[M],ne[M],idx;
int w[N];
int fa[N][K],d[N]; //倍增和lca
PII q[N];//路径
vector<PII> op[N];//记录操作
int ans[N],sum[N*3];
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs_fa(int u,int father,int depth)
{
    d[u]=depth;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==father) continue;
        fa[j][0]=u; //j走一步到u
        for(int k=1;k<K;k++) //处理递增数组
        {
            fa[j][k]=fa[fa[j][k-1]][k-1];
        }
        dfs_fa(j,u,depth+1); //继续搜索下面的节点
    }
}
int lca(int a,int b)
{
    if(d[a]<d[b]) swap(a,b);
    for(int k=K-1;k>=0;k--)
    {
        if(d[fa[a][k]]>=d[b]) 
        {
            a=fa[a][k];
        }
    }
    if(a==b) return a;
    for(int k=K-1;k>=0;k--)
    {
        if(fa[a][k]!=fa[b][k]) 
        {
            a=fa[a][k],b=fa[b][k];
        }
    }
    return fa[a][0];
}
void dfs_sum(int u,int father,int sign)
{
    int t=w[u]+sign*d[u]+M,cnt=sum[t]; 
    for(auto item:op[u]) //计算当前节点
    {
        sum[item.x+M]+=item.y;
    }
    for(int i=h[u];i!=-1;i=ne[i]) //计算树
    {
        int j=e[i];
        if(j==father) continue;
        dfs_sum(j,u,sign);
    }
    ans[u]+=sum[t]-cnt; //总共的减去上面的
}
void work_up() //上链的差分操作
{
    for(int i=0;i<m;i++)
    {
        int a=q[i].x,b=q[i].y;
        int p=lca(a,b);
        int t=d[a];
        op[a].push_back({t,1}); //对路径进行差分操作
        op[fa[p][0]].push_back({t,-1});
    }
    dfs_sum(1,-1,1);
}
void work_down() //下链的差分操作
{
    for(int i=0;i<=n;i++) op[i].clear();
    memset(sum,0,sizeof sum);
    for(int i=0;i<m;i++)
    {
        int a=q[i].x,b=q[i].y;
        int p=lca(a,b);
        int t=d[a]-d[p]*2;
        op[b].push_back({t,1});
        op[p].push_back({t,-1});
    }
    dfs_sum(1,-1,-1);
}
int main()
{
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);
    for(int i=0;i<n-1;i++)
    {
        int a,b;
        scanf("%d %d",&a,&b);
        add(a,b),add(b,a);
    }
    for(int i=1;i<=n;i++) 
    {
        scanf("%d",&w[i]);
    }
    for(int i=0;i<m;i++) 
    {
        scanf("%d%d",&q[i].x,&q[i].y);
    }
    dfs_fa(1,-1,1);
    work_up();
    work_down();
    for(int i=1;i<=n;i++) 
    {
        printf("%d ",ans[i]);
    }
    return 0;
}