$O(n)$

主要是找基环树中环的长度,由于每个点只有一个指向,当我们a->b的时候，a一定是所代表并查集的根,然后我们可以使用带权并查集来维护。

#include<bits/stdc++.h>
using namespace std;
const int N=200010;
int n;
int p[N],d[N];
int find(int x)
{
    if(p[x]!=x)
    {
        int r=find(p[x]);
        d[x]+=d[p[x]];
        p[x]=r;
    }
    return p[x];
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        p[i]=i;
    }
    int res=n;
    for(int i=1;i<=n;i++)
    {
        int t;
        cin>>t;
        int a=i,b=find(t); //合并的时候a一定是代表集合的根
        if(a!=b) //维护带权并查集
        {
            p[a]=b;
            d[a]=d[t]+1;
        }
        else
        {
            res=min(res,d[t]+1);
        }
    }
    cout<<res;
    return 0;
}

$O(n)$

由题意，我们需要在所有点的出度均是1的有向图中，求出最小环的长度。

在有向图中找环有很多算法，比如求有向图强联通分量的Tarian算法等，但杀鸡焉用幸牛刀，这个图很特殊，我们可以使用迭代的方式来做。

注意当题目中点数很大时，如果能用迭代的方式，就尽量不要使用递归的方式，因为可能存在爆栈的问题。

首先我们考虑一下所有点的出度均是1的有向图的性质，其中的每个连通块的形状都是这样的:

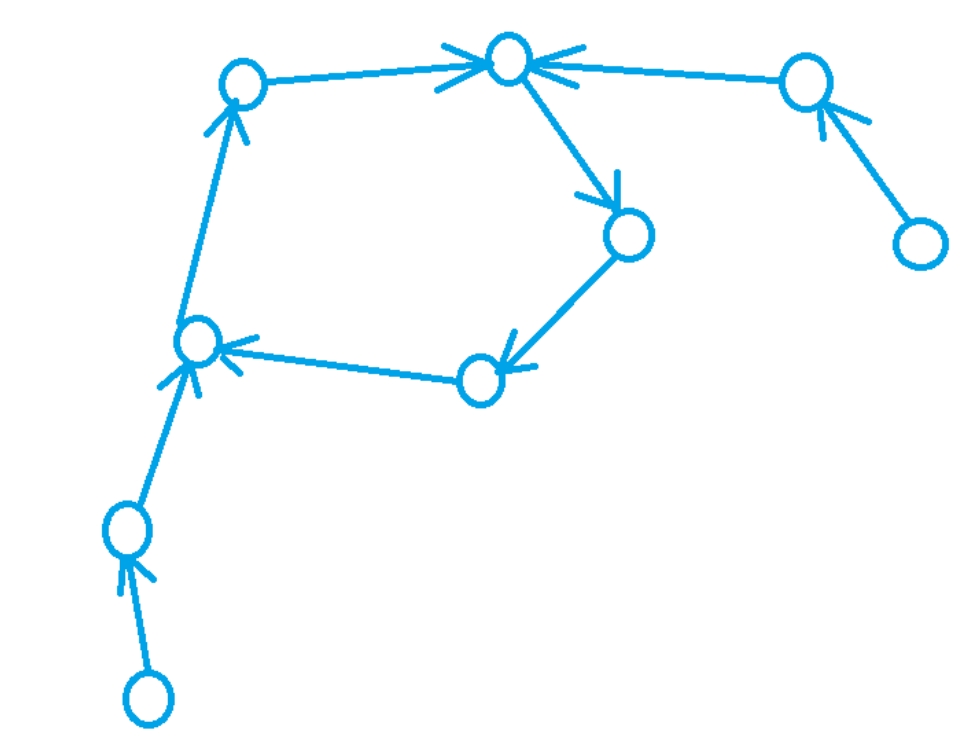
即一个环上挂着很多树，而且不管从哪个点出发，最终都会走到某个环上。

因此我们可以借助于栈结构来找出所有环

从前往后扫描每个点，如果当前点没有被遍历过，则沿着出边一直走，直到走到已经被遍历过的点为止，走的过程中将所有点按顺序存入栈中。此时会有两种情况

此时走到的已被遍历过的点在栈中，则栈中从该点开始，到当前点这部分就是环上的所有点;

此时走到的已被遍历过的点不在栈中，则说明当前只是在某个分支上走，并没有走到某个环上;

所有环的长度的最小值即是答案。

#include<bits/stdc++.h>
using namespace std;
const int N=200010;
int n;
int p[N];
bool st[N],in_stk[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>p[i];
    
    int res=n;
    for(int i=1;i<=n;i++)
    {
        if(!st[i])
        {
            stack<int> stk;
            int j=i;
            while(!st[j]) //还没有走到某个环上
            {
                stk.push(j); //加入边
                st[j]=true; //已经走过
                in_stk[j]=true; //在栈中
                j=p[j]; //去下个点
            }
            if(in_stk[j]) //说明当前点走到j是一个环
            {
                int cnt=1; //当前点到j
                while(stk.top()!=j) //还没有退回到j
                {
                    in_stk[stk.top()]=false; //不在栈中
                    stk.pop();
                    cnt++; //边的个数增加
                }
                res=min(res,cnt);
            }
            while(!stk.empty())  //清空栈中元素
            {
                in_stk[stk.top()]=false;
                stk.pop();
            }
        }
    }
    cout<<res;
    return 0;
}