题目背景

2025 年 06 月 GESP C++ 七级编程第 1 题

题目描述

给定由 $n$ 个结点与 $m$ 条边构成的简单无向图 $G$，结点依次以 $1,2,\dots,n$ 编号。简单无向图意味着 $G$ 中不包含重边与自环。$G$ 的线图 $L(G)$ 通过以下方式构建：

• 初始时线图 $L(G)$ 为空。

• 对于无向图 $G$ 中的一条边，在线图 $L(G)$ 中加入与之对应的一个结点。

• 对于无向图 $G$ 中两条不同的边 $(u_1,v_1),(u_2,v_2)$，若存在 $G$ 中的结点同时连接这两条边（即 $u_1,v_1$ 之一与 $u_2,v_2$ 之一相同），则在线图 $L(G)$ 中加入一条无向边，连接 $(u_1,v_1),(u_2,v_2)$ 在线图中对应的结点。

请你求出线图 $L(G)$ 中所包含的无向边的数量。

输入格式

第一行，两个正整数 $n,m$，分别表示无向图 $G$ 中的结点数和边数。

接下来 $m$ 行，每行两个正整数 $u_i,v_i$，表示 $G$ 中连接 $u_i,v_i$ 的一条无向边。

输出格式

输出共一行，一个整数，表示线图 $L(G)$ 中所包含的无向边的数量。

样例

5 4
1 2
2 3
3 1
4 5

3

5 10
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5

30

说明/提示

【样例解释 #1】

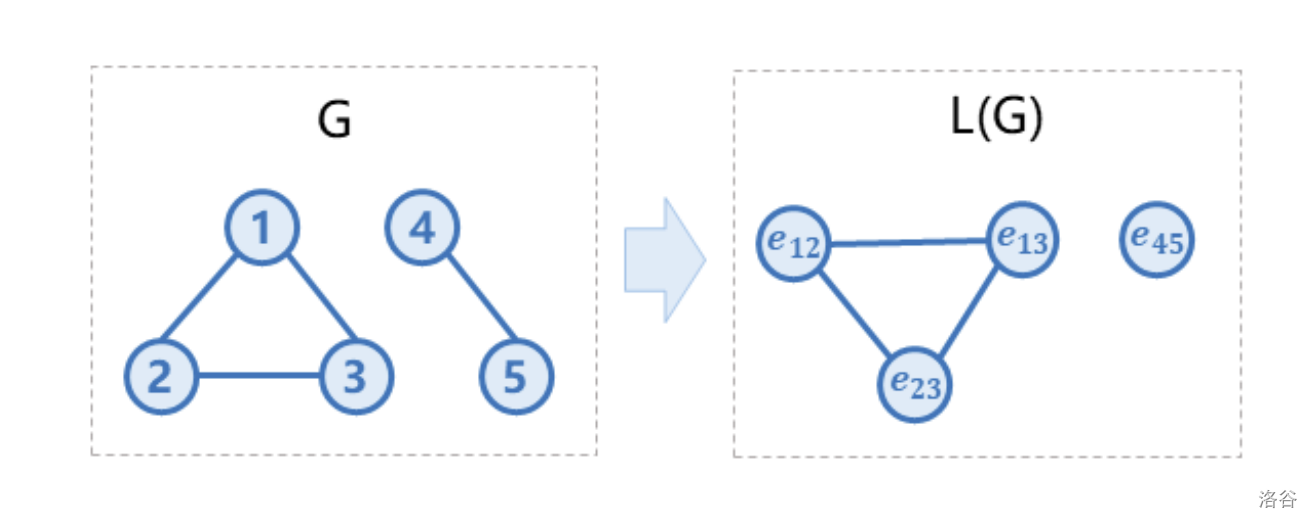
数据范围

对于 $60\%$ 的测试点，保证 $1 \le n \le 500,1 \le m \le 500$。

对于所有测试点，保证 $1 \le n \le 10^5,1 \le m \le 10^5$。